¿Cuando nos interesa usar más la correlación que la causalidad?

La estadística, como ciencia de los datos, aborda su recolección, estructuración, análisis e interpretación, en particular cuando la variabilidad y la incertidumbre son inherentes. Algunos de estos conceptos se están poniendo muy de moda en el marketing, pero también se pueden usar en más ramas, algunos de ellos han salido de la medicina por ejemplo.

Podremos tomar decisiones con una mayor probabilidad de acierto basado en datos 

¿Qué es una correlación?

Vamos a empezar hablando de que son las correlaciones, que estas no dejan de ser la relación que tenemos entre dos o más variables. Este punto es importante porque podemos controlar por ejemplo la relación que hay entre número de visitas que tenemos a nuestra web y las conversiones, por ejemplo, a más visitas en nuestra web de un usuario es más probable que convierta. 

¿Qué métodos podemos utilizar para las correlaciones?

Tenemos varias formas para poder calcular estas correlaciones en nuestros proyectos, a continuación, veremos cuales son las más conocidas y utilizadas para el cálculo de correlaciones.

Covarianza:

La covarianza nos muestra qué relación puede haber entre dos variables, en este caso, si sale positivo es porque la relación que tenemos entre el valor mayor de la variable 1 y el mayor de la variable 2 tienen relación y comprobamos que tienen un comportamiento similar.

Por el contrario, si los valores altos tienen relación con los valores mínimos este nos dará un valor negativo. Si por el contrario tuviéramos un 0 como valor, esto significa que no tenemos relación entre las variables.

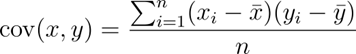
Coeficiente de correlación de Pearson:

El coeficiente de correlación de Pearson es una relación de dependencia lineal entre dos variables. La diferencia entre la correlación de Pearson y la covarianza es que es independiente de la escala de medida de las variables.

Esta correlación la usamos para definir el grado de relación entre dos variables siempre y cuando sean cuantitativas y continuas.

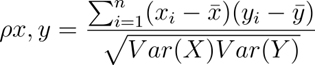
Si el valor resultado de aplicar la fórmula es 1, lo que nos indica es que la relación entre las dos variables es perfecta.

Además, tenemos otro valor que es el p_value que nos dice si la correlación que tenemos es estadísticamente significativa.

¿Qué es el p_value y cómo se interpreta?

El p_value es un dato que nos va a indicar entre 0 y 1 que tan probable es observar ciertos resultados bajo una condición específica. Además, este dato nos dirá si son iguales o más inusuales que el resultado que hemos obtenido en el experimento. Con esto podemos entender que si el p_value es 0, no hay relación entre el primer valor y el segundo. En definitiva, el p_value no es una probabilidad como tal, de que una hipótesis sea o no cierta, sino más bien de cuán probable es obtener el resultado tan inusual como el que vemos en un caso.

Coeficiente de correlación de Spearman:

Este coeficiente de correlación de Spearman es la medida de asociación entre dos variables, además no necesitamos que sean lineales los datos. Digamos que lo que hace es que, cuando una variable aumenta o disminuye y la segunda también, nos indica que la correlación entre ambas es alta.

A diferencia de la correlación de Pearson también se pueden usar datos ordinales. Con esto es menos sensible a valores extremos o atípicos que nos encontramos muchas veces en nuestros datos.

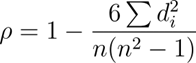
¿Cuándo es más óptimo usar cada método?

La covarianza mide cómo varían conjuntamente dos variables e indica la dirección de su relación (positiva o negativa). No es adecuada para comparar la intensidad de la asociación porque su magnitud depende de las unidades de medida. Para cuantificar la fuerza de una relación lineal entre variables cuantitativas usamos la correlación de Pearson, recomendable cuando la relación es aproximadamente lineal, no hay valores atípicos relevantes y, idealmente, las variables siguen una distribución normal. Si existen valores atípicos, la relación es monótona pero no lineal, o trabajamos con datos ordinales o sin normalidad, es preferible la correlación de Spearman.

¿Qué es un modelo causal?

Los modelos causales son herramientas para representar y explicar cómo unas variables (causas) influyen en otras (efectos) dentro de un sistema. A diferencia de la correlación, que solo mide asociación, los modelos causales permiten estimar el efecto de intervenir en una variable sobre las demás.

Estos modelos causales se representan por DAGs (diagramas de causalidad) que son nodos donde veríamos las variables y las flechas para indicar relaciones de causa y efecto como por ejemplo el gasto en publicidad y las ventas. Otra forma de representarlos es a través de ecuaciones estructurales (SEM) que nos permite especificar ecuaciones que relacionan las variables causales con sus efectos, incluyendo errores o perturbaciones que explican variaciones no observadas.

¿Que es una inferencia causal?

La inferencia causal es el conjunto de métodos que usamos para saber el efecto de una acción sobre un resultado en concreto. Básicamente respondería a la pregunta de ¿qué pasaría si hacemos este cambio en la variable?

Experimentos areatolizados:

Un ensayo controlado aleatorizado (RCT, por sus siglas en inglés) consiste en asignar al azar a los participantes a un grupo de tratamiento o a un grupo de control para identificar el efecto causal. La aleatorización garantiza que, salvo por recibir la intervención, ambos grupos sean comparables en promedio; así, cualquier diferencia en los resultados puede atribuirse al tratamiento.

Diseños Cuasi-experimentales:

Cuando no tenemos la opción de realizar experimentos aleatorios, se utilizan técnicas como el matching, la regresión de discontinuidad o las diferencias de diferencias (DiD) para imitar las condiciones de un experimento y controlar posibles variables.

El matching o emparejamiento consiste en la asignación de cada sujeto del grupo de tratamiento con uno del grupo de control que tenga características similares. Así intentamos que las diferencias observadas se produzcan por el tratamiento aplicado y no por diferencias preexistentes.

Con la regresión de discontinuidad aprovechamos un punto de corte natural en los datos. Por ejemplo, en marketing, podrían compararse los clientes que ofrecen una mayor puntuación a cierto valor, otorgándole a éstos un beneficio. A partir de ahí, se compararían los clientes que están solo por encima y justo por debajo del nivel. La idea es que estos dos grupos sean muy similares excepto por el hecho de haber recibido o no el beneficio.

Diferencias en diferencias analizan la evolución de dos grupos en dos periodos, antes y después de aplicar la intervención.

Modelos Basados en datos observacionales:

Este sería el más conocido, ya que lo vemos también en herramientas como pueden ser Google Analytics 4 o Google Ads. Usando los métodos estadísticos y de algoritmos de machine learning, se pueden estimar los efectos a partir de datos que no provienen de experimentos controlados normalmente sino de datos históricos de los proyectos. Estos incluyen el uso de variables instrumentales o técnicas de control sintético.

Conclusión

La correlación y la causalidad se complementan, pero responden a preguntas distintas. La correlación (con Pearson o Spearman según supuestos) es idónea para explorar y monitorizar relaciones entre variables, priorizar hipótesis y detectar patrones; la covarianza solo orienta sobre dirección, no sobre intensidad comparable. Cuando el objetivo es estimar el efecto de una intervención y fundamentar decisiones (por ejemplo, “¿qué pasa si aumento el presupuesto de publicidad?”), necesitamos modelos y métodos causales: idealmente RCTs, y, cuando no son viables, diseños cuasi-experimentales (matching, discontinuidad, DiD) o modelos con datos observacionales (p. ej., variables instrumentales o control sintético) con supuestos explícitos. En la práctica, conviene usar la correlación para generar y priorizar hipótesis y la inferencia causal para atribuir impactos y optimizar acciones. Así, el análisis pasa de “qué se mueve con qué” a “qué causa qué”, mejorando la calidad de las decisiones en marketing y en otros ámbitos.

Éstas pueden ser herramientas muy potentes a tener en cuenta, por ejemplo, en campañas de PPC (Pay Per Clic).

Podéis encontrar un ejemplo de códigos básicos que muestran cómo interactúan los datos en diferentes momentos: https://github.com/pichu2707/corr-causal-enae